Diary - Log

Provide for a rainy day.

未雨绸缪

Updated time: 11/23 2023.

Ref

1. wikipedia

2. The first Brillouin zone of a (simple) hexagonal lattice (I thought it provided wrong messages)

3. Materials Cloud

4. doi: 10.1016/j.commatsci.2010.05.010

0. Introduction

Analysis procedure: POSCAR ==>> Reciprocal vector/ K-space ==>> K-mesh

Note: The key discussion is the different K-mesh between primitive cell and conventional cell

1. A general problem is how to generate K-mesh in VASP software

I got an OUTCAR file, but I couldn’t understand all the meaning of it.

1.0 reciprocal vector is strange

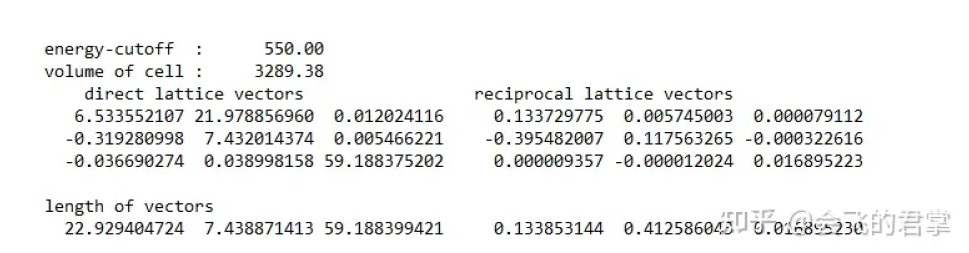
why it is? How to calculate it?

1.1 Irreducible k-points

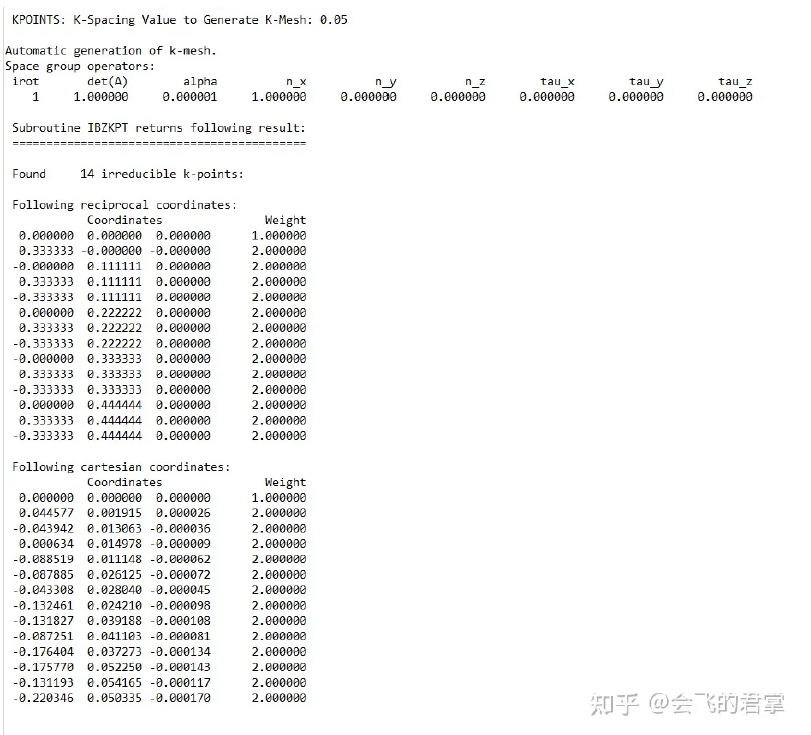
In my POSCAR, there are two primitive cells along a₁. But in reciprocal space, the k-points along the b1 direction are almost irreducible, and those along the b₂ direction are reduced.

Why? I try to solve it by using Matlab.

2. Constructing of the k-space

clear
clc

Public symbol

% 指定要生成的感叹号符号的数量
numExclamationPoints = 20;
numNotPoints = 40;
% 使用循环生成感叹号符号
exclamationString = '';
for i = 1:numExclamationPoints
    exclamationString = [exclamationString '!'];
end
% 使用循环生成分割线符号
noteString = '';
for i = 1:numNotPoints
    noteString = [noteString '-'];
end

Now, Calculating of reciprocal vectors and its length

% 输入：正晶格基矢量矩阵 A
% 输出：包含倒晶格基矢量的矩阵 B, 长度 lengths

%% 功能
% 1. 从正晶格到倒易晶格
% 2. 手动输入基矢量矩阵，并检查基矢量独立性

%% 未完成功能
% 1. 输入格式多样，

% 从用户获取正晶格基矢量,并检查基矢量的独立性
prompt = "Please input the matix of direct-vector (row by row):\n" + ...
         "Please don't forget character []\n";
while true
    disp(noteString)
    A = input(prompt);
    % 检查基矢量的线性独立性
    if det(A) < 3
        disp(exclamationString);
        disp('The base vector is dependent');
        disp(noteString)
    else
        disp('The base vector is independent');
        disp('Direct vector')
        disp(A)
        disp(noteString)
        break; % 如果矢量是线性独立的，退出循环
    end
end


% 1. 计算正晶格的体积
V = det(A);

% 2. 计算倒晶格基矢量矩阵，矢量定义和矩阵求逆,两种单位1/Angstron,2*pi/Angstron
%    A*B'=2*pi*I; B=2*pi*inv(A)'
%    注意 B 矩阵的转置
% % B = zeros(3, 3);
% % for i = 1:3
% %     B(i, :) = (2*pi/V) * cross(A(mod(i,3)+1, :), A(mod(i+1,3)+1, :));
% % end
B1 = 2*pi*inv(A)';
B2 = inv(A)'

% 使用norm函数计算每一行矢量的长度
lengths_B1 = zeros(1, size(B1, 1));
lengths_B2 = zeros(1, size(B2, 1));
for i = 1:size(B1, 1)
    lengths_B1(i) = norm(B1(i, :));
end
for i = 1:size(B2, 1)
    lengths_B2(i) = norm(B2(i, :));
end

% 3. 验证是否为对角矩阵 2*pi，这也是前面为什么可以求逆
disp(noteString)
disp("Please check it if it's a diagonal matrix")
disp("units:Angstron X 1/Angstron")
disp(B1*A')
disp(noteString)
disp("units:Angstron X 2*pi/Angstron")
disp(B2*A')
disp(noteString)

% 得到的矩阵 B 就是包含倒晶格基矢量的矩阵
disp(noteString)
disp('Reciprocal vectors (units:1/Angstron):')
disp(B1)
disp('The length of Rec-Vectors')
disp(lengths_B1)
disp(noteString)
disp("Reciprocal vectors (units:2*pi/Angstron):")
disp(B2)
disp('The length of Rec-Vectors')
disp(lengths_B2)
disp(noteString)

The matrix of the reciprocal vector has two equivalent definitions, vector operations and matrix transformations. The latter is recommended, B = inv(A)'or B = 2·pi·inv(A)', depending on units (2·pi·1/Angstron or 1/Angstron).

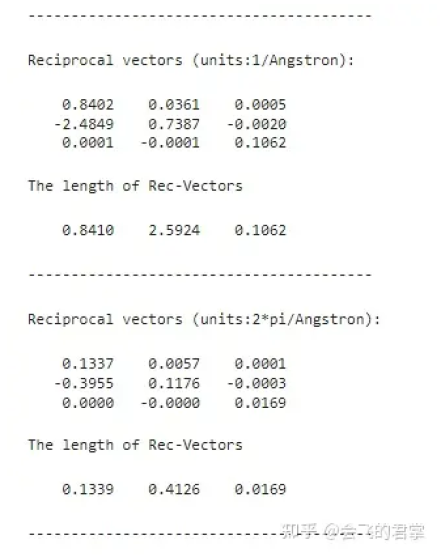
3. Generating K-mesh

First, we must know the definition of the first Brillouin zone, [-0.5, -0.5, -0.5] to [0.5, 0.5, 0.5] in the units scale.

Second, we need to transform from k-points resolved values to the density of k-mesh.

Third, if we want to get a gamma-centered k-mesh, just shift the center to the gamma point [0, 0, 0]. Obviously, the number along the 3-direction should be odd.

Obatian Gamma-centered K-mesh

% Input: KPT-Resolved Value (e.g., 0.04, in unit of 2*PI/Angstrom)
% Output: The matrix of kpoints

%% 功能
% 1. 输入两种 KPR value, 并检查格式
% 2. 分割中心对称网格,如果是偶数则加一


% 从用户获取网格精度
prompt = ['Please input the KPT-Resolved Value (e.g., 0.01 < 0.04 < 0.06, in unit of 2*PI/Angstrom):\n' ...
    'Please input the KPT-Resolved Value (e.g., 10 < 25 < 100, in unit of 1/Angstrom):\n'];
temp = 0;
while true
    temp = input(prompt);
    % 检查基矢量的线性独立性
    if (temp < 0.06) && (temp > 0.01)
        disp('The KPR value is reasonable');
        disp('KPR value')
        kpr = 1.0/temp
        disp(kpr)
        break;
    elseif temp < 100 && temp > 10
        disp('The KPR value is reasonable');
        disp('KPR value')
        kpr = temp
        disp(kpr)
        break; % 如果矢量是线性独立的，退出循环
    else
        disp(exclamationString);
        disp('The kpr value is too high or too low!');
    end
end

Obviously, the number along the 3-direction should be odd.

N = round(max(1,lengths_B1/(2*pi/kpr)));
N = N + ~mod(N,2)

The results are [3 9 1] , but in OUTCAR, the irreducible points are 14 (2+4*3). The k-points along b₂ is reduced!

4. Resulting from symmetry

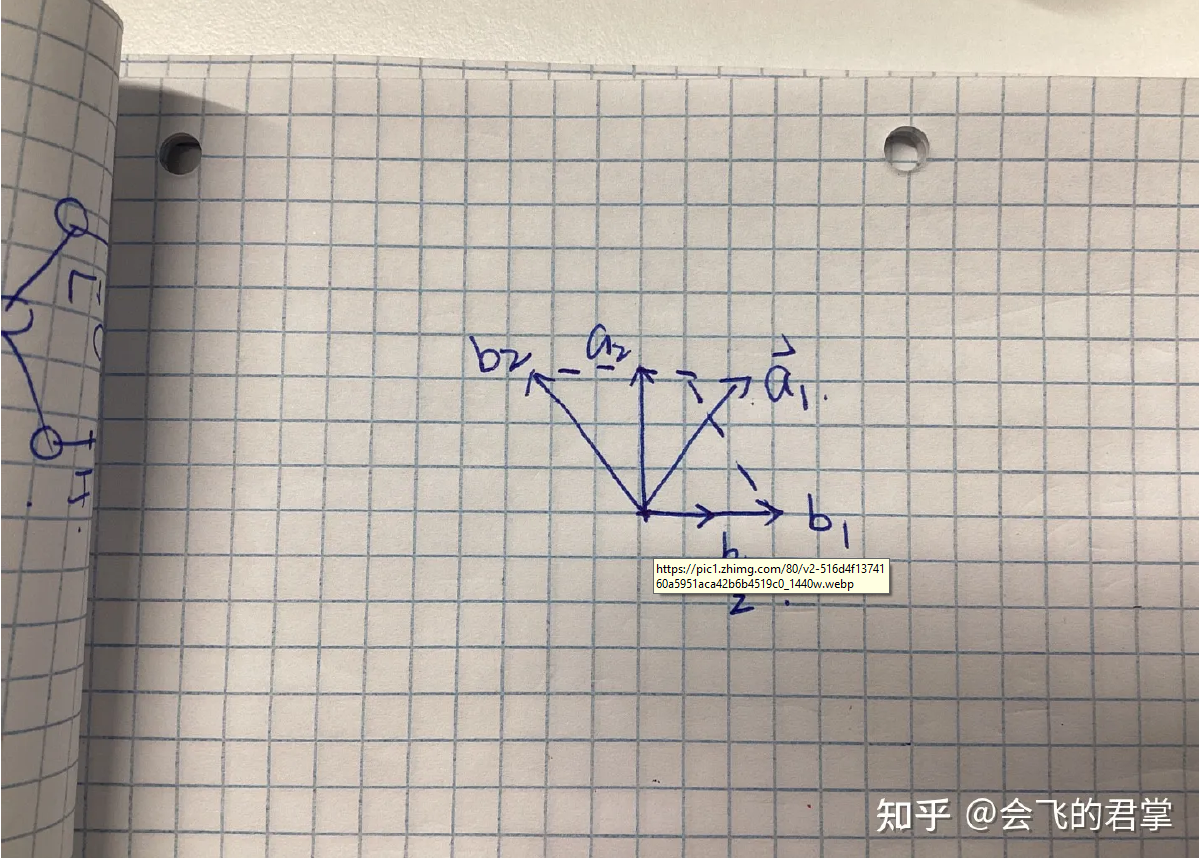
b₀₁, b₀₂, b₀₃ is reciprocal basis vector of the primitive cell.

b₁₁, b₁₂, b₁₃ is reciprocal basis vector of the conventional cell.

a₀₁…

a₁₁…

a₁₁ = 2·a₀₁, a₁₂ = a₀₂, a₁₃ = a₀₃.

so, b₁₁ = 0.5·b₀₁, b₁₂ = b₀₂, b₁₃ = b₀₃.

Then, the symmetry along the b₁₁ direction is broken. Those along other direction is reserved.

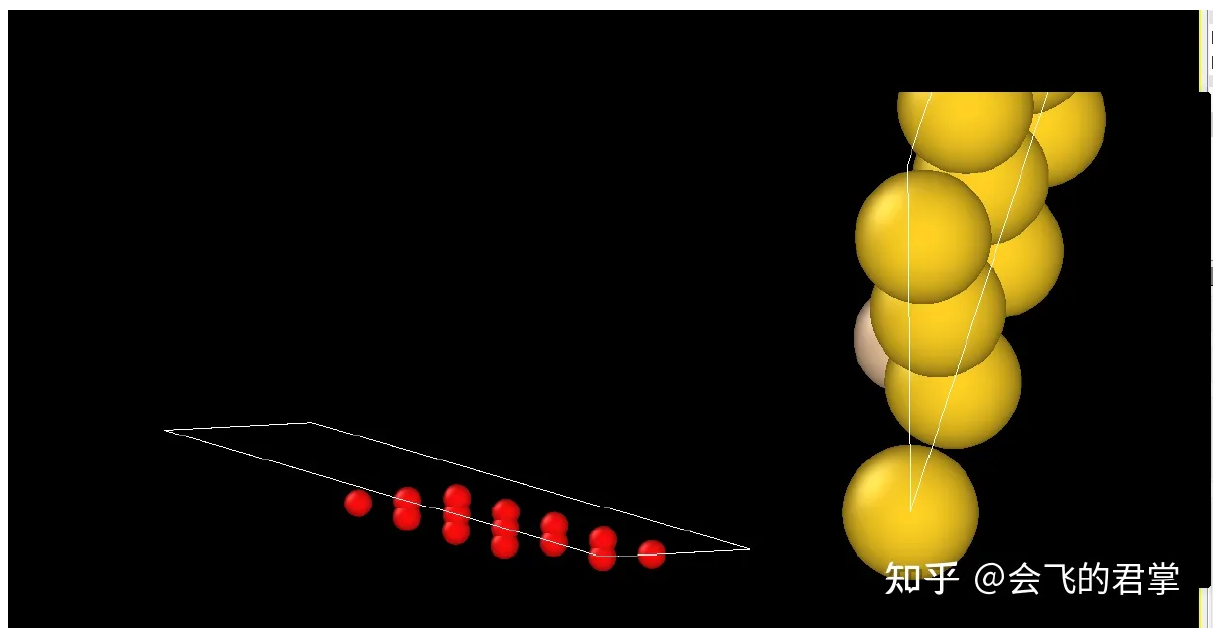
5. SeekPath: A useful tool to visualize the Brillouin zone of any crystals.

Even then, it could be used to find a primitive cell!

6. An interesting literature about high-symmetry points/path.

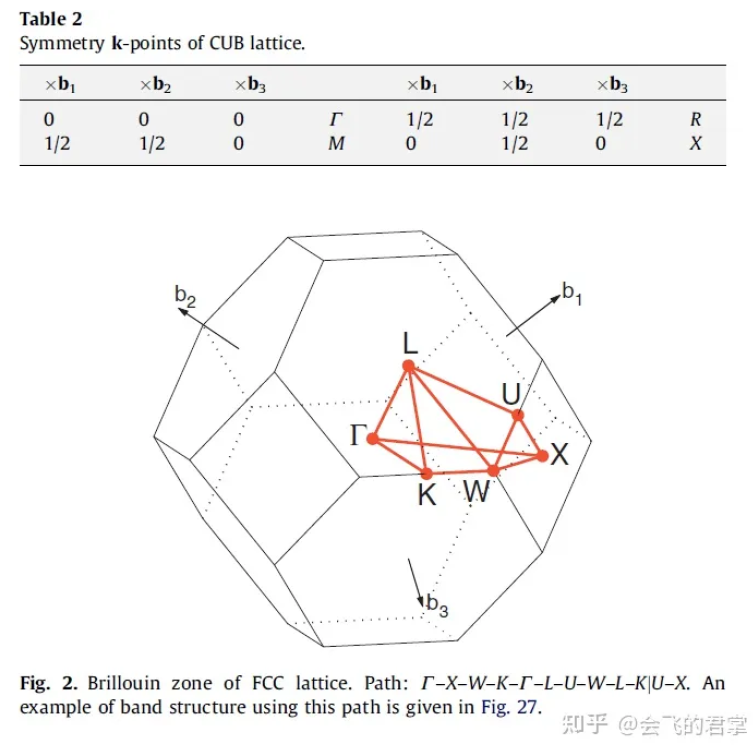
They draw some brillouin zone of many lattices. It’s interesting.

At the end

• Solved:

  • Matlab code, Done
  • Generating reducible K-points, Done

• Not solved:

  • Generating irreducible K-points

---

Please indicate the source when reprinting. Please verify the citation sources in the article and point out any errors or unclear expressions.