Good wine needs no bush.
酒好不怕巷子深
Updated time: 11/21 2023.
K 空间是什么
Ref:Highlight 为本文主要参考
1. 一张二维衍射图
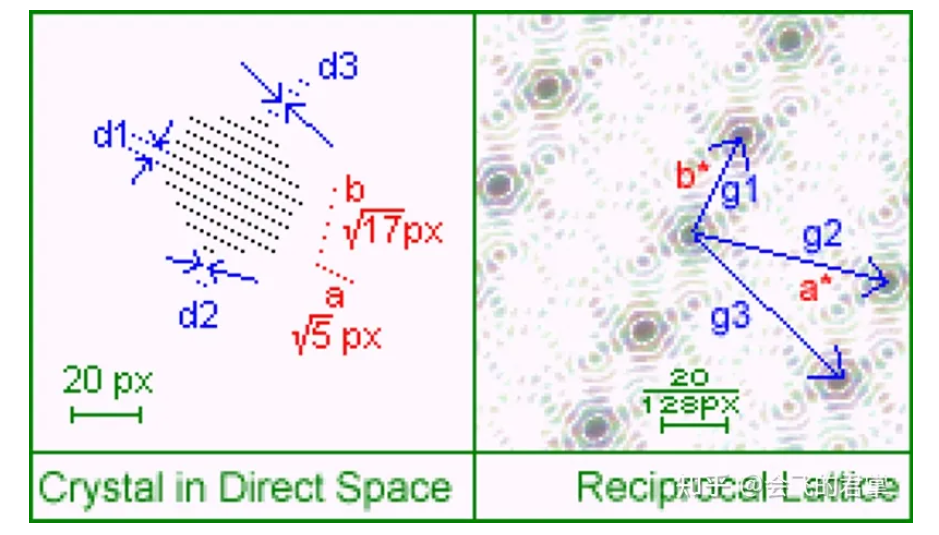
二维晶格中,正、倒易基矢量互相垂直。三维晶格,只有正晶格基矢量互为垂直,才满足上述关系。
倒易矢量方向垂直于晶格面—-沿晶格间距方向,大小与间距成反比,见节2。d1>d2=d3,所以g2=g3>g1 。
倒易空间中 g1 方向为1系列点,对应晶格间距为 d1, 2·d1, 3·d1…的波矢都在第一布里渊区中。这也是我们为什么这么关心第一布里渊区的原因。
正空间中,位置的量纲为 [L],倒空间中波矢的量纲为 [L-1] ,见节2。
2. 一个简单的数学描述,布拉格定律和布洛赫函数
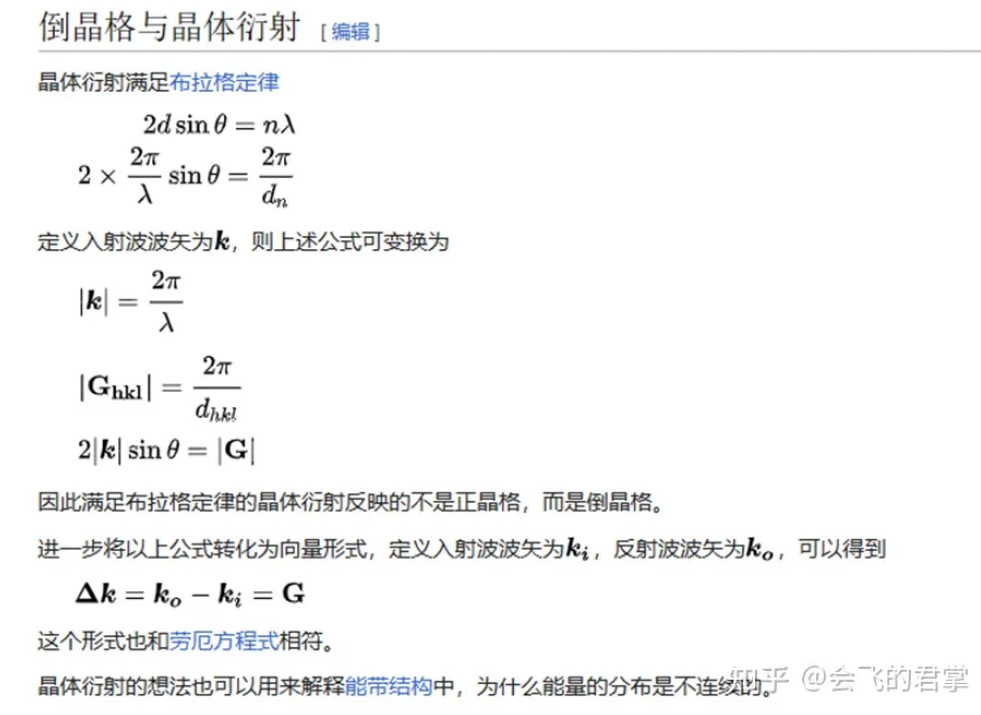
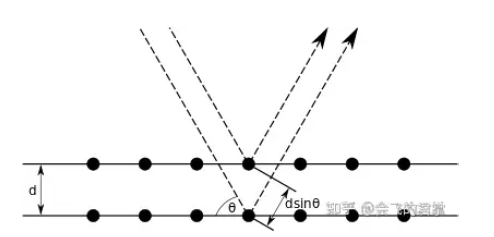
晶体衍射实验,可以从入射波和反射波的波矢,方向,相位确定反射平面方向和晶面间距。由此,满足布拉格定律的晶体衍射反映的不是正晶格而是倒晶格。
联想到一维原子链的晶格间距为a,倒晶格间距为2·pi/a。我们可以想象一束特定波矢的波沿原子链方向入反射,记录下了原子间距的信息。

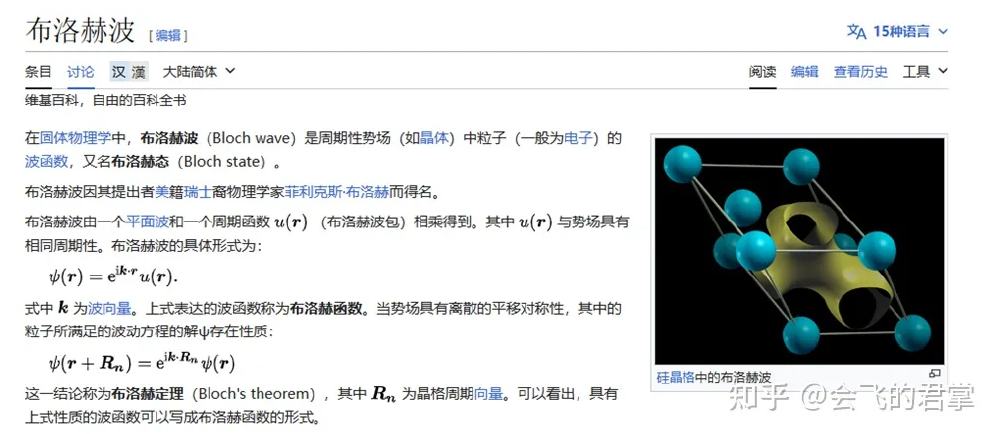
p 和 k 只差一个常数因子,所以倒易空间也称动量空间。另外,p = h·k在晶体中不成立。
布洛赫波由一个平面波和一个周期函数相乘得到。
3. 一个形而上学的解释

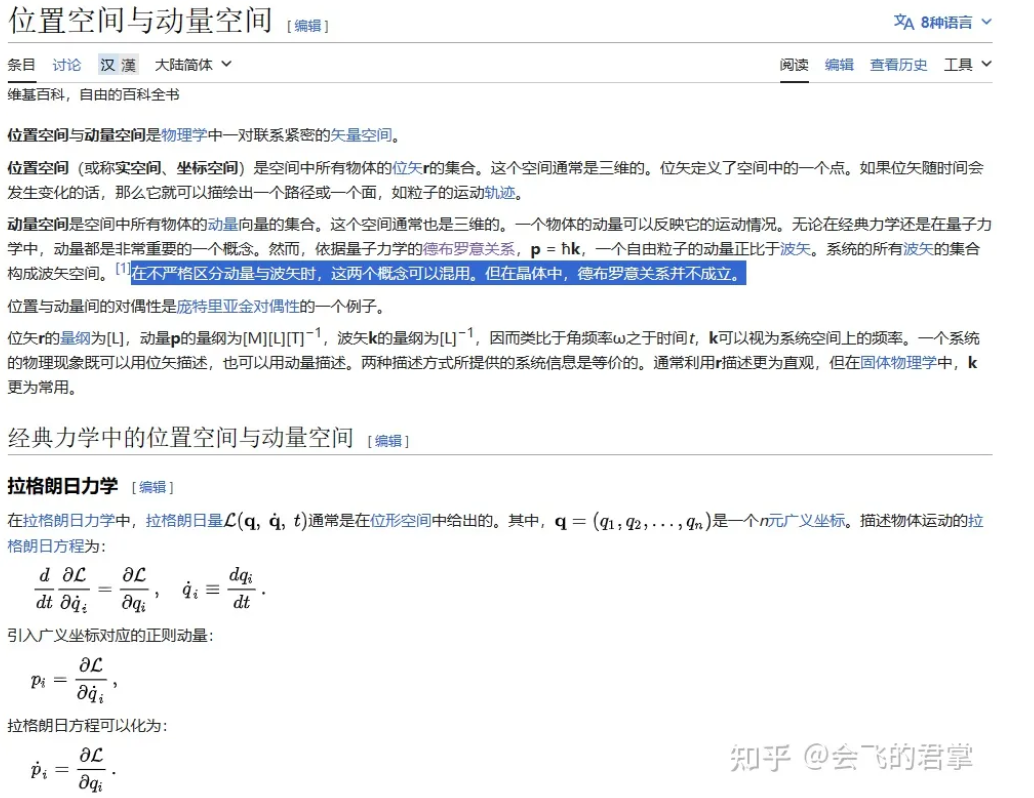
类似于时域和频域的对偶,傅里叶变换可以从位置空间描述到动量描述的转换。类比于角频率之于时间 t,k 可以视为系统空间上的频率。我的理解是对于不同的晶格类型,有不同的满足布洛赫衍射的波矢,由此将波矢作为该晶格类型的一种描述。类似的频域分析也是,找到共振频率,进而分析。
我还联想到的是波粒二象性,光既不是粒子也不是波,但他有两种属性,都是实验测得的。而原子经典意义上是一个粒子,但在原子与原子的联系中又有波的性质,例如相互作用力。世界上的相互作用都是波性质的体现,因为两个原子不会紧密的接触在一起(除了密排金属),通过相互作用互相排斥或吸引。而密排金属并不是没有相互作用,恰恰相反,不然他们为啥会吸引在一起呢。只是能量最低的结构,以及能垒高低不同而已。经典力学是个宏观的概念,在原子尺度,他可以解释一些弹性阶段的事,比如将两个原子近似为弹簧连接,但远离平衡状态的现象却没法很好的解释。任何一种理论都有其特定的局限性。我觉得密度泛函理论是很普适的,也只是因为我没接触到更本征的领域而已。
4. 布里渊区
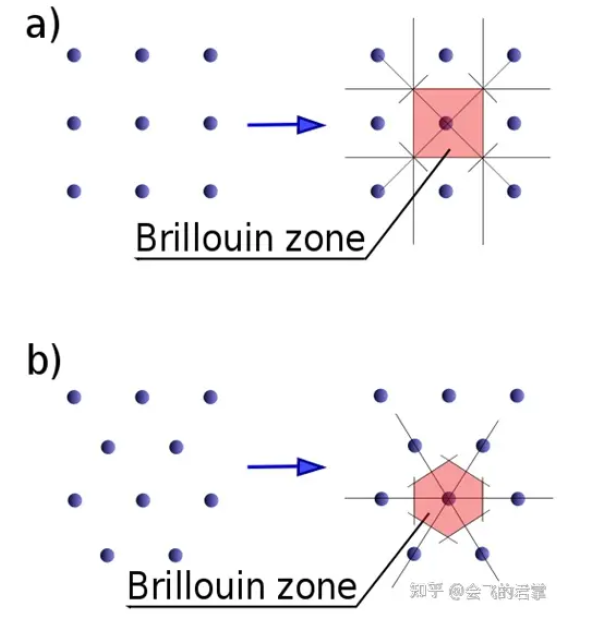

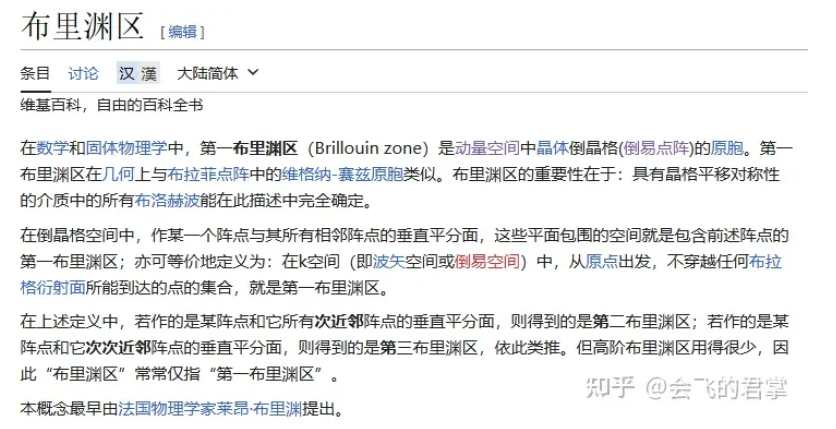


我觉得参考8中的不同晶格的倒晶格对我最容易接受。
5. 一些没有解决的问题和碎碎念
我是为了复现 VASP 中关于 K 点的划分而查这么多资料的。
POSCAR 为原胞和超胞对 K 点的划分影响吗?
POSCAR 中 a1 方向有两个原胞,但划分网格时反而 b2 方向缩减了 k 点,为什么?
差一张图,HCP 晶格的倒晶格还是 HCP,高对称路径。
/_|差不多是这个三角形,但是各个高对称点的含义和名字我不清楚。
解决的问题
看到了衍射空间,写了一篇文章方便复习,做了 PPT 整理
了解了些许物理含义,对偶。。。甚至看到了分析力学,勒让德变换,我一直以为这是经典力学的范畴
正在写 matlab 代码,就差最后一步 k 点划分了
对三维晶格倒空间第一布里渊区的高对称点有了个直观的概念,通俗的讲就是根据对称性去折叠,沿着折叠的轨迹去算。
Please indicate the source when reprinting. Please verify the citation sources in the article and point out any errors or unclear expressions.